Lời giải bài tập 1.21 SGK Toán 12 Tập 1

Lời giải bài tập 1.21 SGK Toán 12 Tập 1 KNTT, trang 32 về nội dung: Khảo sát sự biến thiên và vẽ đồ thị hàm số. Giải bài tập 1.21. a) Ta c...

Lời giải bài tập 1.21 SGK Toán 12 Tập 1 KNTT, trang 32 về nội dung: Khảo sát sự biến thiên và vẽ đồ thị hàm số.

Giải bài tập 1.21. a)

Ta có: ${y}'=-3{{x}^{2}}+3$, ${y}'=0$ khi $x=\pm 1$.
+ Hàm số đồng biến trên khoảng $\left( -1;1 \right)$ và nghịch biến trên từng khoảng $\left( -\infty ;-1 \right)$và $\left( 1;+\infty \right).$
+ Hàm số đạt cực đại tại $x=1$ với ${{y}_{C}}=3$, đạt cực tiểu tại $x=-1$ với ${{y}_{CT}}=-1$.
+ Giới hạn tại vô cực: $\displaystyle \underset{x\to -\infty }{\mathop{\lim }}\,y=+\infty $, $\displaystyle \underset{x\to +\infty }{\mathop{\lim }}\,y=-\infty $.
+ Bảng biến thiên:

+ Đồ thị: Đồ thị hàm số cắt trục tung tại điểm $\left( 0;1 \right),$điểm này đồng thời là tâm đối xứng của đồ thị.

Giải bài tập 1.21. b)

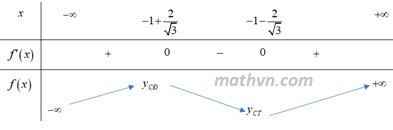
Ta có: ${y}'=3{{x}^{2}}+6x-1$. Do đó ${y}'=0$ khi $x={{x}_{1}}=-1+\dfrac{2}{\sqrt{3}}$ hoặc $x={{x}_{2}}=-1-\dfrac{2}{\sqrt{3}}$.
+ Hàm số đồng biến trên từng khoảng $\left( -\infty ;{{x}_{1}} \right)$ và $\left( {{x}_{2}};+\infty \right)$.
+ Hàm số đạt cực đại tại $x={{x}_{1}}$ với ${{y}_{C}}=f\left( {{x}_{1}} \right),$ đạt cực tiểu tại $x={{x}_{2}}$ với ${{y}_{CT}}=f\left( {{x}_{2}} \right)$.
+ Giới hạn tại vô cực: $\displaystyle \underset{x\to -\infty }{\mathop{\lim }}\,f\left( x \right)=-\infty $, $\displaystyle \underset{x\to +\infty }{\mathop{\lim }}\,f\left( x \right)=+\infty $.
+ Bảng biến thiên:

+ Đồ thị: Đồ thị hàm số cắt trục tung tại điểm $\left( 0;-1 \right)$, có tâm đối xứng là điểm $\left( -1;2 \right)$.